已知椭圆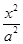 +
+ =1(a>b>0)的左、右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=
=1(a>b>0)的左、右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=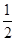
(1)求椭圆的标准方程;
(2)若P是椭圆上的任意一点,求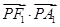 的取值范围;
的取值范围;
(3)已知直线l:y=kx+m与椭圆相交于不同的两点M,N(均不是长轴的端点),AH⊥MN,垂足为H且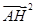 =
= ,求证:直线l恒过定点.
,求证:直线l恒过定点.
化简: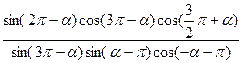 。
。
(本小题满分15分)
已知A、B、C是直线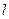 上的不同的三点,O是直线外一点,向量
上的不同的三点,O是直线外一点,向量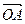 、
、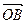 、
、 满足
满足 ,记
,记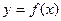 .
.
(1)求函数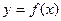 的解析式;
的解析式;
(2)若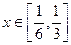 ,
,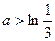 ,证明:不等式
,证明:不等式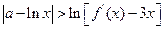 成立;
成立;
(3)若关于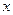 的方程
的方程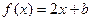 在
在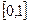 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数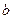 的取值范围.
的取值范围.
已知椭圆 和抛物线
和抛物线 有公共焦点F(1,0),
有公共焦点F(1,0),  的中心和
的中心和 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线 与抛物线
与抛物线 分别相交于A,B两点.
分别相交于A,B两点.
(Ⅰ)写出抛物线 的标准方程;
的标准方程;
(Ⅱ)若 ,求直线
,求直线 的方程;
的方程;
(Ⅲ)若坐标原点 关于直线
关于直线 的对称点
的对称点 在抛物线
在抛物线 上,直线
上,直线 与椭圆
与椭圆 有公共点,求椭圆
有公共点,求椭圆 的长轴长的最小值.
的长轴长的最小值.
(本小题满分14分)
如图,三棱柱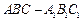 中,侧面
中,侧面
 底面
底面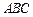 ,
, ,
,
且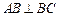 ,O为
,O为 中点.
中点.
(Ⅰ)证明: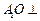 平面
平面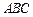 ;
;
(Ⅱ)求直线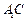 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在 上是否存在一点
上是否存在一点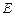 ,使得
,使得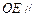 平面
平面 ,若不存在,说明理由;若存在,
,若不存在,说明理由;若存在,
确定点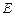 的位置.
的位置.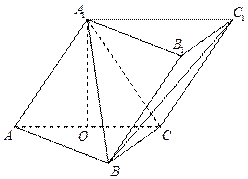
(本小题满分14分)
某人上楼梯,每步上一阶的概率为,每步上二阶的概率,设该人从台阶下的平台开始出发,到达第n阶的概率为Pn.
(I)求P2;
(II)该人共走了5,求该人这5步共上的阶数x的数学期望.