P为圆A: 上的动点,点
上的动点,点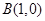 .线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
.线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
(1)求曲线Γ的方程;
(2)当点P在第一象限,且 时,求点M的坐标.
时,求点M的坐标.
在平面直角坐标系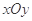 中,动点
中,动点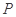 到两点
到两点 ,
, 的距离之和等于
的距离之和等于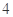 ,设点
,设点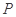 的轨迹为曲线
的轨迹为曲线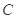 ,直线
,直线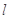 过点
过点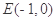 且与曲线
且与曲线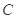 交于
交于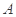 ,
,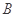 两点.
两点.
(1)求曲线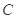 的轨迹方程;
的轨迹方程;
(2)是否存在△ 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△ 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
设数列{an}的前n项和为Sn,且 ,n=1,2,3
,n=1,2,3
(1)求a1,a2;
(2)求Sn与Sn﹣1(n≥2)的关系式,并证明数列{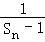 }是等差数列;
}是等差数列;
(3)求S1•S2•S3 S2011•S2012的值.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形, ,
, ,平面
,平面 底面
底面 ,
, 为
为 中点,M是棱PC上的点,
中点,M是棱PC上的点, .
.
(1)若点M是棱PC的中点,求证: 平面
平面 ;
;
(2)求证:平面 底面
底面 ;
;
(3)若二面角M-BQ-C为 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
在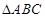 中,角
中,角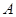 、
、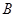 、
、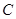 所对的边分别为
所对的边分别为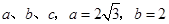 ,
,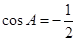 .
.
(1)求角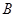 的大小;
的大小;
(2)若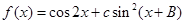 ,求函数
,求函数 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.