（本题12分）有4个不同的小球，4个不同的盒子，现需把球全部放进盒子里，
（1）没有空盒子的方法共有多少种？
（2）可以有空盒子的方法共有多少种？
（3）恰有1个盒子不放球，共有多少种方法？（最后结果用数字作答）
（本题12分）已知复数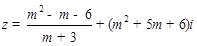
（1）m取什么值时，z是实数？
（2）m 取什么值时，z是纯虚数？
（本小题满分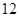
分）某校高二年级某班的数学课外活动小组中有6名男生，4名女生，从中选出4人参加数学竞赛考试，用X表示其中的男生人数，求X的分布列。
（本小题14分）已知中心在原点，焦点在
轴上的椭圆
的离心率为
，且经过点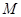
．
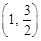（Ⅰ）求椭圆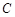的方程；
（Ⅱ）是否存过点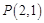
的直线
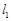与椭圆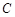相交于不同的两点
，满足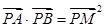
？若存在，求出直线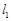的方程；若不存在，请说明理由．
（本小题12分）已知函数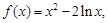
（Ⅰ）求函数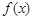
的极值；
（Ⅱ）设函数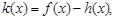
若函数
在
上恰有两个不同零点，求实数
的取值范围．
求证：
； 
在区间（0，2）内至少有一个零点；