已知函数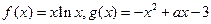 .
.
(Ⅰ)求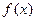 在
在 上的最小值;
上的最小值;
(Ⅱ)若存在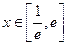 (
( 是常数,
是常数, =2.71828
=2.71828 )使不等式
)使不等式 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)证明对一切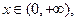 都有
都有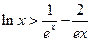 成立.
成立.
已知数列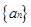 的前
的前 项和为
项和为 ,且满足:
,且满足: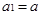
 ,
,
 N*,
N*,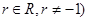 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若存在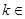 N*,使得
N*,使得 ,
,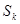 ,
, 成等差数列,试判断:对于任意的
成等差数列,试判断:对于任意的 N*,且
N*,且 ,
, ,
, ,
,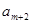 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论.
设函数 (1)求
(1)求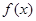 的单调递增区间. (2)已知函数
的单调递增区间. (2)已知函数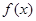 的图象在点A(
的图象在点A(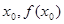 )处,切线斜率为
)处,切线斜率为 ,求:
,求: 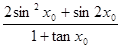
已知函数f(x)=aln x-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2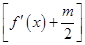 (f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: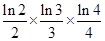 ×…×
×…× <
< (n≥2,n∈N*).
(n≥2,n∈N*).
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于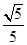 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
如图,在四棱锥A—BCC1B1中,等边三角形ABC所在平面与正方形BCC1B1所在平面互相垂直,D为CC1的中点.
(1)求证:BD⊥AB1;
(2)求二面角B—AD—B1的余弦值.