(本小题满分12分)如图,已知正三棱柱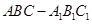 的各棱长都是4,
的各棱长都是4, 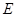 是
是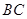 的中点,动点
的中点,动点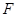 在侧棱
在侧棱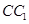 上,且不与点
上,且不与点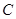 重合.
重合.
(I)当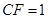 时,求证:
时,求证: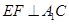 ;
;
(II)设二面角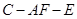 的大小为
的大小为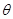 ,求
,求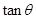 的最小值.
的最小值.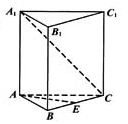
袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.
(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求点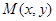 满足
满足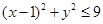 的概率.
的概率.
函数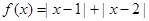
(1)画出函数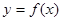 的图象;
的图象;
(2)若不等式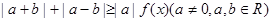 恒成立,求实数
恒成立,求实数 的范围.
的范围.
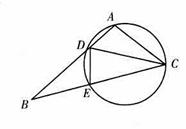
如图,四边形 是圆内接四边形,延长
是圆内接四边形,延长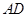 与的延长线
与的延长线 交于点
交于点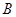 ,且
,且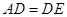 ,
, 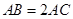 .
.
(1)求证: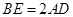 ;
;
(2)当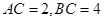 时,求
时,求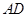 的长.
的长.
已知函数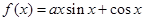 ,且
,且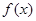 在
在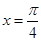 处的切线斜率为
处的切线斜率为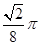 .
.
(1)求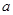 的值,并讨论
的值,并讨论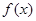 在
在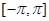 上的单调性;
上的单调性;
(2)设函数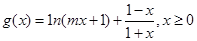 ,其中
,其中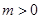 ,若对任意的
,若对任意的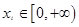 总存在
总存在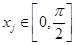 ,使得
,使得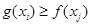 成立,求
成立,求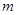 的取值范围.
的取值范围.
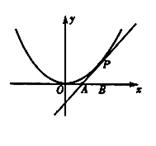
如图,已知直线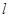 与抛物线
与抛物线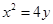 相切于点
相切于点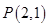 ,且与
,且与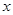 轴交于点
轴交于点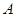 ,
,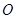 为坐标原点,定点
为坐标原点,定点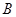 的坐标为
的坐标为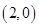 .
. 
(1)若动点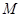 满足
满足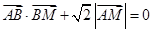 ,求点
,求点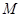 的轨迹
的轨迹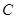 ;
;
(2)若过点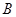 的直线
的直线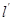 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹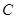 交于不同的两点
交于不同的两点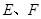 (
(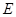 在
在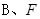 之间),试求△OBE与△OBF面积之比的取值范围.
之间),试求△OBE与△OBF面积之比的取值范围.