(本小题满分14分)已知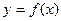 (
( ,
,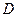 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数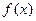 在
在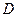 内单调递增或单调递减;②如果存在区间
内单调递增或单调递减;②如果存在区间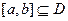 ,使函数
,使函数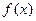 在区间
在区间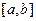 上的值域为
上的值域为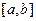 ,那么称
,那么称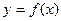 ,
, 为闭函数;
为闭函数;
请解答以下问题:
(1) 求闭函数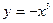 符合条件②的区间
符合条件②的区间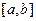 ;
;
(2) 判断函数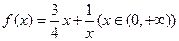 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若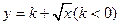 是闭函数,求实数
是闭函数,求实数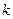 的取值范围;
的取值范围;
已知命题 :函数
:函数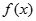 为
为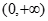 上单调减函数,实数
上单调减函数,实数 满足不等式
满足不等式 .命题
.命题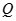 :当
:当 ,函数
,函数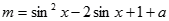 .若命题
.若命题 是命题
是命题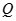 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围。
的取值范围。
设函数 .
.
(Ⅰ)求函数y=f(x)的最小值.
(Ⅱ)若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知圆C的极坐标方程为 ,直线l的参数方程为
,直线l的参数方程为 (t为常数,t∈R)
(t为常数,t∈R)
(Ⅰ)求直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)求直线l与圆C相交的弦长.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB关于x的方程 的两个根.
的两个根.
(Ⅰ)证明:C、B、D、E四点共圆;
(Ⅱ)若∠A=90°,且m=4,n=6,求C、B、D、E所在圆的半径.
已知函数 ,其中a∈R,
,其中a∈R,
(Ⅰ)若a=0,求函数f(x)的定义域和极值;
(Ⅱ)当a=1时,试确定函数 的零点个数,并证明.
的零点个数,并证明.