(本题满分12分,第1小题6分,第小题6分)
设函数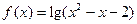 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。
(1)求A∩B;
(2)若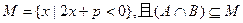 ,求实数
,求实数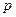 的取值范围。
的取值范围。
(本小题满分10分)某班主任对班级22名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多.
(1)根据以上数据建立一个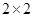 列联表;
列联表;
(2)试问喜欢电脑游戏与认为作业多少是否有关系?
(12分)设函数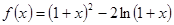 .(1)求
.(1)求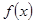 的单调区间;(2)当
的单调区间;(2)当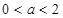 时,求函数
时,求函数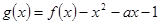 在区间
在区间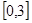 上的最小值.
上的最小值.
(12分)已知函数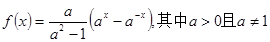
(1)判断函数的奇偶性和单调性;
(2)当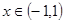 时,有
时,有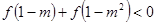 ,求
,求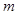 的取值范围.
的取值范围.
(12分)已知函数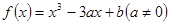
(1)若曲线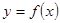 在点
在点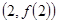 处与直线
处与直线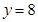 相切,求
相切,求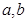 的值;
的值;
(2)求函数 的单调区间与极值.
的单调区间与极值.
.(12分)飞机每飞行1小时的费用由两部分组成,固定部分为4900元,变动部分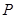 (元)与飞机飞行速度
(元)与飞机飞行速度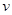 (千米∕小时)的函数关系式是
(千米∕小时)的函数关系式是 ,已知甲乙两地的距离为
,已知甲乙两地的距离为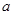 (千米).
(千米).
(1)试写出飞机从甲地飞到乙地的总费用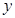 (元)关于速度
(元)关于速度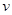 (千米∕小时)的函数关系式;
(千米∕小时)的函数关系式;
(2)当飞机飞行速度为多少时,所需费用最少?