如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB＝a（a>2），BC＝2，且AE＝AH＝CF＝CG，设AE＝x，绿地面积为y．
(Ⅰ)写出y关于x的函数关系式，并指出这个函数的定义域；
(Ⅱ)当AE为何值时，绿地面积最大？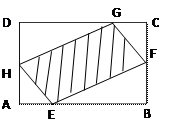
如图，已知一艘船从30 n mile/h的速度往北偏东
的Ａ岛行驶，计划到达Ａ岛后停留10 min后继续驶往Ｂ岛，Ｂ岛在Ａ岛的北偏西
的方向上．船到达Ｃ处时是上午10时整，此时测得Ｂ岛在北偏西
的方向，经过20 min到达Ｄ处，测得Ｂ岛在北偏西
的方向，如果一切正常的话，此船何时能到达Ｂ岛？
 |
经过两点
，
，且在
轴上截得的弦长为
的圆的方程．
如图（１）是某条公共汽车线路收支差额
与乘客量
的图象．
（１）试说明图（１）上点
、点
以及射线
上的点的实际意义；
（２）由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，
如图（２）（３）所示．你能根据图象，说明这两种建议是什么吗？
求与两坐标轴正向围成面积为２平方单位的三角形，并且两截距之差为３的直线的方程．
求证：梯形两条对角线的中点连线平行于上、下底，且等于两底差的一半（用解析法证之）．