(本小题满分14分)
设数列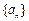 的前
的前 项和为
项和为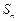 ,且
,且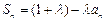
 ,其中
,其中 为常数,
为常数, .
.
(1)求证:数列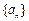 是等比数列;
是等比数列;
(2)若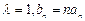 ,数列
,数列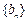 的前
的前 项和为
项和为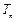 ,求证:当
,求证:当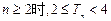 ;
;
(3)设数列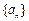 的公比为
的公比为 数列
数列 满足
满足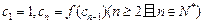 求证:
求证: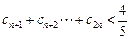 .
.
在区间[-1,1]上任取两数a、b,求二次方程x2+ax+b=0的两根
(1)都是实数的概率;
(2)都是正数的概率.
在等腰Rt△ABC中,在斜边AB上任取一点M,求AM的长小于AC的长的概率.
如图3-3-16所示,在长为4、宽为2的矩形中有一以矩形的长为直径的半圆,试用随机模拟法近似计算半圆的面积,并估计π的值.
图3-3-16
在长为12 cm的线段AB上任取一点M,并以线段AM为边作正方形.试求这个正方形的面积介于36 cm2和81 cm2之间的概率.有条件的同学可以用计算机或计算器模拟这个试验,并且估计所求随机事件的概率.
利用随机模拟方法计算图3-3-14中阴影部分(y=x3和x=2以及x轴所围成的部分)的面积.
图3-3-14