某种商品在近30天内每件的销售价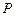 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足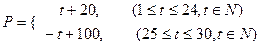 ,商品的日销售量
,商品的日销售量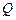 (件)与时间
(件)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足 ,求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中第几天?
,求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中第几天?
(本小题满分12分)如图,在平面直角坐标系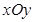 中,点
中,点 ,直线
,直线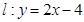 ,设圆
,设圆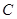 的半径为
的半径为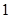 ,圆心在
,圆心在 上.
上.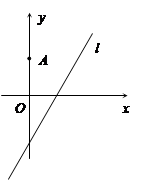
(Ⅰ)若圆心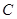 也在直线
也在直线 上,过点
上,过点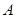 作圆
作圆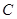 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅱ)若圆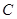 上存在点
上存在点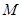 ,使
,使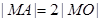 ,求圆心
,求圆心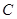 的横坐标
的横坐标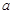 的取值范围.
的取值范围.
(本小题满分12分)如图,四面体 中,
中,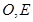 分别
分别 的中点,
的中点,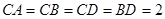 ,
, .
.
(Ⅰ)求证:AO⊥平面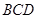 ;
;
(Ⅱ)求异面直线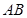 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离.
(本小题满分12分)设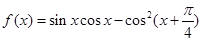 .
.
(Ⅰ)求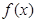 的单调区间;
的单调区间;
(Ⅱ)在锐角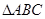 中,角
中,角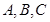 的对边分别为
的对边分别为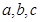 ,若
,若 ,求
,求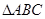 面积的最大值.
面积的最大值.
(本小题满分10分)设圆上的点 关于直线
关于直线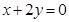 的对称点仍在圆上,且与直线
的对称点仍在圆上,且与直线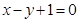 相交的弦长为
相交的弦长为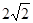 ,求圆的方程.
,求圆的方程.
已知关于x,y的方程C: .
.
(1)当m为何值时,方程C表示圆.
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且MN= ,求m的值.
,求m的值.