如图所示,左图是杭州儿童乐园中的过山车的实物图片,右图是过山车的原理图.在原理图中,半径分别为R1="2.0" m和R2="8.0" m的两个光滑圆形轨道固定在倾角为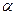 =37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量
=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使质量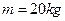 的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为
的小车(视作质点)从P点以一定的初速度沿斜轨道向下运动.已知斜轨道面与小车间的动摩擦因数为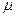 =
=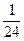 ,g="10" m/s2,sin 37°="0.6,cos" 37°=0.8.问:
,g="10" m/s2,sin 37°="0.6,cos" 37°=0.8.问:
(1)若小车能通过A、B两点,则小车在P点的初速度满足什么条件?
(2)若小车恰好能通过第二个圆形轨道的最高点B,则小车通过第一个圆形轨道最低点
时,对轨道的压力大小是多少?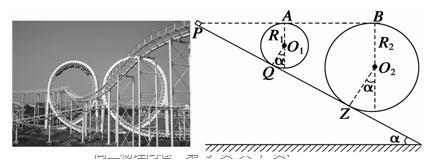
分)(秋如图所示,一斜面体A放在水平地面上,其截面为广直角三角形.物块B被一与水平面成θ角的外力挤压在斜面体的右侧面上,当外力的大小为F时,物块B刚好不能下滑,此时斜面体处于静止状态.已知斜面体A与物块B的质量分别为M和m,重力加速度为g,求: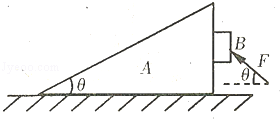
(1)物块B受到的摩擦力的大小;
(2)地面对斜面体A的摩擦力及地面对斜面体A的支持力的大小.
如图所示,一质量m1=0.6kg的小车静止在光滑的水平面上,现有一质量m2="0.3" kg的物块,以水平向右的速度v0="6" m/s从左端滑上小车,最后在车面上某处与小车保持相对静止。物块与车面间的动摩擦因数0.4,取g="10" m/s2,求:
(1)物块与小车的共同速度v。
(2)物块在车面上滑行的时间t。
如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球。此装置以速度v0=2m/s向右滑动。另一质量也为M的滑块静止于上述装置的右侧。当两滑块相撞后,便粘在一起向右运动,求
(1)两滑块相撞过程中损失的机械能。
(2)当小球向右摆到最大高度时,两滑块的速度大小。
如图所示,某潜水员在检查装有透明液体的圆柱体容器,当潜水员的眼睛在容器中心轴位置且在液面下h2=1m处时,他看到容器口处所有景物都出现在一个顶角为60°的倒立圆锥里,已知容器口距离容器液面的距离h1=1m,圆柱体的横切面半径 。
。
①求容器中液体的折射率。
②若一个身高h3=1m的小孩站在离容器口边缘 远的位置,小孩恰好能看到对面的容器底部,则容器中液体的深度为多少米?
远的位置,小孩恰好能看到对面的容器底部,则容器中液体的深度为多少米?
(9分)一列简谐横波沿直线传播,在这条直线上相距d=1.5m的A、B两点的震动图像分别如图甲、乙所示。已知波长λ>1m,求这列波的波速v.