（本小题满分12分）
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分PC，且分别交AC、PC于D、E两点，又PB=BC，PA="A" B．
（Ⅰ）求证：PC⊥平面BDE；
（Ⅱ）若点Q是线段PA上任一点，求证：BD⊥DQ；
（Ⅲ）求线段PA上点Q的位置，使得PC//平面BDQ．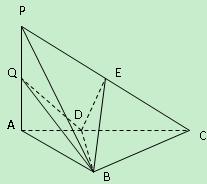
(本题满分14分)
已知椭圆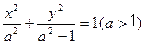
的左右焦点为
，抛物线C：
以F2为焦点且与椭圆相交于点M，直线F1M与抛物线C相切。
（Ⅰ）求抛物线C的方程和点M的坐标；
（Ⅱ）过F2作抛物线C的两条互相垂直的弦AB、DE，设弦AB、DE的中点分别为F、N，求证直线FN恒过定点；
（本小题满分14分）
某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为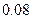
，只选修甲和乙的概率是
，至少选修一门的概率是
，用
表示小张选修的课程门数和没有选修的课程门数的乘积.
（Ⅰ）求学生小张选修甲的概率；
（Ⅱ）记“函数
为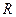
上的偶函数”为事件
，求事件的概率；
（Ⅲ）求的分布列和数学期望。
（本小题满分12分）
如图，在三棱锥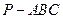
中，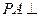
底面ABC,
，
AP="AC," 点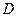
，
分别在棱
上，且BC//平面ADE
（Ⅰ）求
证：DE⊥平面
；
（Ⅱ）当二面角
为直二面角时，求多面体ABCED与PAED的体积比。
（本小题满分12分）
已知函数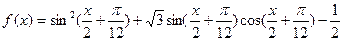
。
（Ⅰ）求
的值域；
（Ⅱ）若（x>0）的图象与直线
交点的横坐标由小到大依次是
，
，…，
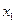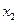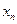，求数列
的前
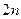项的和。
（本小题满分14分）
已知函数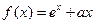
，
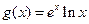.（其中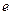
为自然对数的底数），
（Ⅰ）设曲线
在
处的切线与直线
垂直，求
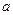的值；
（Ⅱ）若对于任意实数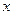
≥0，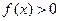
恒成立，试确定实数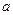的取值范围；
（Ⅲ）当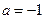
时，是否存在实数
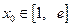，使
曲线C：
在点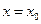
处的切线与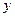
轴垂直？若存在，求出
的值；若不存在，请说明理由.