(满分12分) 函数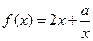 的定义域为(0,1](
的定义域为(0,1]( 为实数).
为实数).
(1)当 时,求函数
时,求函数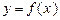 的值域,
的值域,
(2)当 时,求函数
时,求函数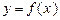 在
在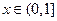 上的最小值,并求出函数取最小值时
上的最小值,并求出函数取最小值时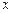 的值.
的值.
已知函数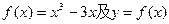 上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求
上一点P(1,-2),过点P作直线l,(Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程;(Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);(Ⅲ)在(Ⅱ)的条件下,求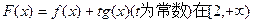 上单调时,t的取值范围.
上单调时,t的取值范围.
如图,矩形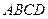 中,
中,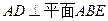 ,
,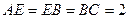 ,
,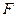 为
为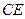 上的点,且
上的点,且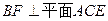 .
.
(Ⅰ)求证: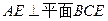 ;(Ⅱ)求证;
;(Ⅱ)求证;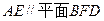 ;
;
(Ⅲ)求三棱锥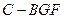 的体积.
的体积.
已知向量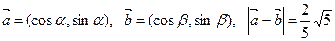 ,
,
(Ⅰ)求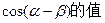 ;(Ⅱ)若
;(Ⅱ)若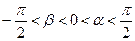 ,且
,且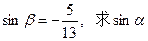 的值.
的值.
已知函数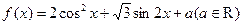 .(1)若x∈R,求f(x)的单调递增区间;(2)若x∈[0,
.(1)若x∈R,求f(x)的单调递增区间;(2)若x∈[0,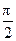 ]时,f(x)的最大值为4,求a的值,并指出这时x的值
]时,f(x)的最大值为4,求a的值,并指出这时x的值
(本题满分15分)已知数列{ }中
}中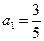 ,
,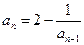 (n≥2,
(n≥2,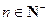 ),数列
),数列 ,满足
,满足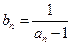 (
(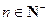 )(1)求证数列{
)(1)求证数列{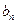 }是等差数列;(2)求数列{
}是等差数列;(2)求数列{ }中的最大项与最小项,并说明理由(3)记
}中的最大项与最小项,并说明理由(3)记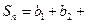 …
…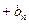 ,求
,求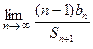 .
.