(本小题满分13分)已知函数
(I)若函数 在
在 时取到极值,求实数
时取到极值,求实数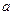 的值;
的值;
(II)试讨论函数 的单调性;
的单调性;
(III)当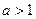 时,在曲线
时,在曲线 上是否存在这样的两点A,B,使得在点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,若存在,试求
上是否存在这样的两点A,B,使得在点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,若存在,试求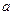 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)
已知点 是椭圆
是椭圆 上任意一点
上任意一点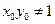 ,直线
,直线 的方程为
的方程为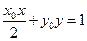
(I)判断直线 与椭圆E交点的个数;
与椭圆E交点的个数;
(II)直线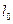 过P点与直线
过P点与直线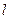 垂直,点M(-1,0)关于直线
垂直,点M(-1,0)关于直线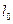 的对称点为N,直线PN恒
的对称点为N,直线PN恒
过一定点G,求点G的坐标。
如图,平面ABEF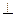 平面ABCD,四边形ABEF与ABCD都是直角梯形,
平面ABCD,四边形ABEF与ABCD都是直角梯形,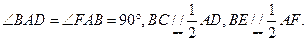
(I)证明:C,D,F,E四点共面;
(II)设AB=BC=BE,求二面角A—ED—B的大小。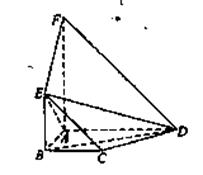
(本小题满分12分)
已知 的三
的三 内角A,B,C所对三边分别为a,b,c,且
内角A,B,C所对三边分别为a,b,c,且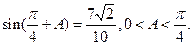
(I)求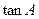 的值。
的值。
(II)若 的面积
的面积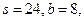 求a的值。
求a的值。
(本小题满分12分)一射击测试每人射击三次,每击中目标一次记10分。没有击中记0分,某人每次击中目标的概率为
(I)求此人得20分的概率;(I I)求此人得分的数学期望与方差。
I)求此人得分的数学期望与方差。
(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个白球,乙盒内有大小相同的2个红球和4个白球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为白球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.