(本小题满分14分)在平面直角坐标系中,已知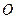 为坐标原点,点
为坐标原点,点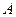 的坐标为
的坐标为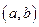 ,点
,点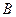 的坐标为
的坐标为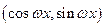 ,其中
,其中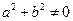 且
且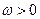 .设
.设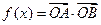 .
.
(I)若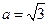 ,
,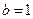 ,
,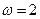 ,求方程
,求方程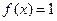 在区间
在区间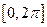 内的解集;
内的解集;
(II)若点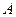 是曲线
是曲线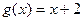 上的动点.当
上的动点.当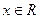 时,设函数
时,设函数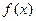 的值域为集合
的值域为集合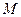 ,不等式
,不等式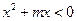 的解集为集合
的解集为集合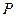 . 若
. 若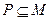 恒成立,求实数
恒成立,求实数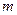 的最大值;
的最大值;
(III)根据本题条件我们可以知道,函数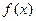 的性质取决于变量
的性质取决于变量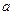 、
、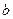 和
和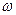 的值. 当
的值. 当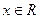 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数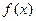 满足“图像关于点
满足“图像关于点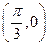 对称,且在
对称,且在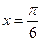 处
处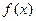 取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
取得最小值”.【说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.】
(本小题满分13 分)
如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
(1)求证:MN//平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P—DB—M 的大小.
(本小题满分12 分)
已知{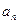 }是整数组成的数列,a1 = 1,且点
}是整数组成的数列,a1 = 1,且点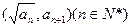 在函数
在函数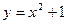 的图象上,
的图象上,
(1)求数列{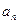 }的通项公式;
}的通项公式;
(2)若数列{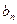 }满足
}满足 = 1,
= 1,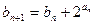 ,求证:
,求证:
(本小题满分12 分)
从甲地到乙地一天共有A、B 两班车,由于雨雪天气的影响,一段时间内A 班车正点到达乙地的概率为0.7,B 班车正点到达乙地的概率为0.75。
(1)有三位游客分别乘坐三天的A 班车,从甲地到乙地,求其中恰有两名游客正点到达的概率(答案用数字表示)。
(2)有两位游客分别乘坐A、B 班车,从甲地到乙地,求其中至少有1 人正点到达的概率(答案用数字表示)。
(本小题满分12 分)
已知函数 的最大值为1.
的最大值为1.
(1)求常数a 的值;
(2)求 的单调递增区间;
的单调递增区间;
(3)求 ≥ 0 成立的x 的取值集合.
≥ 0 成立的x 的取值集合.
(本小题满分14分)如下图(5),在三棱锥 中,
中, 分别是
分别是 的中点,
的中点, ,
, 。
。
(1)求证: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求点 到平面
到平面 的距离。
的距离。