 、
、 两城相距100km,在两地之间 (直线AB上)距
两城相距100km,在两地之间 (直线AB上)距 城
城 km处的
km处的 地建一核电站给
地建一核电站给 、
、 两城供电,为保证城市安全,核电站与城市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数为0.3,若
两城供电,为保证城市安全,核电站与城市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数为0.3,若 城供电量为20亿度/月,
城供电量为20亿度/月, 城为10亿度/月.
城为10亿度/月.
(1)求月供电总费用 表示成
表示成 的函数;
的函数;
(2)核电站建在距A城多远,才能使供电费用最小?
(本题满分l4分)已知向量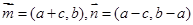 ,且
,且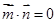 ,其中
,其中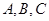 是
是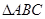 的三内角,
的三内角,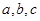 分别是角
分别是角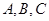 的对边.
的对边.
(1)求角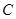 的大小;(2)求
的大小;(2)求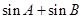 的取值范围.
的取值范围.
设A(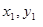 ),B(
),B(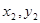 )是椭圆
)是椭圆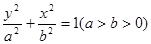 的两点,
的两点,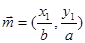 ,
,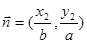 ,且
,且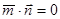 ,椭圆的离心率
,椭圆的离心率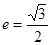 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1)求椭圆方程;
(2)若存在斜率为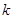 的直线AB过椭圆的焦点F(
的直线AB过椭圆的焦点F(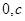 )(
)(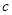 为半焦距),求
为半焦距),求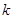 的值;
的值;
(3)试问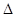 AOB的面积是否为定值?若是,求出该定值;若不是,说明理由。
AOB的面积是否为定值?若是,求出该定值;若不是,说明理由。
已知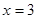 是函数
是函数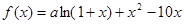 的一个极值点。
的一个极值点。
(1)求 ;(2)求函数
;(2)求函数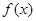 的单调区间;
的单调区间;
(3)若直线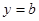 与函数
与函数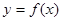 的图象有3个交点,求
的图象有3个交点,求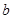 的取值范围。
的取值范围。
(12)设焦点在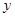 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为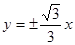 ,且离心率为2,已知点A(
,且离心率为2,已知点A(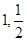 )
)
(1)求双曲线的标准方程;
(2)过点A的直线L交双曲线于M,N两点,点A为线段MN的中点,求直线L方程。
函数 ,过曲线
,过曲线 上的点
上的点 的切线斜率为3.
的切线斜率为3.
(1)若 在
在 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;
(2)在(1)的条件下,求 在
在 上最大值;
上最大值;