(本题12分)已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,
,
向量
 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,试判断
,试判断 取得最大值时
取得最大值时 形状.
形状.
(本小题满分12分)已知方程 的系数a在[0,2]内取值,b在[0,3]内取值,求使方程没有实根的概率.
的系数a在[0,2]内取值,b在[0,3]内取值,求使方程没有实根的概率.
(本小题满分12分)已知棱长为4的正方体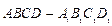 中,
中, 为侧面
为侧面 的中心,
的中心,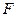 为棱
为棱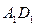 的中点,试计算
的中点,试计算
(1)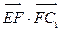 ;
;
(2)求证 面
面 ;
;
(3)求 与面
与面 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)命题P:不等式 对于一切
对于一切 恒成立,命题Q:直线
恒成立,命题Q:直线 经过一、三象限,已知
经过一、三象限,已知 真,
真, 假,求a的取值范围.
假,求a的取值范围.
(本小题满分14分)
已知函数 是一个奇函数.
是一个奇函数.
(1)求 的值和
的值和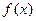 的值域;
的值域;
(2)设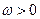 ,若
,若 是区间
是区间 上的增函数,求
上的增函数,求 的取值范围.
的取值范围.
(3)设 ,若对
,若对 取一切实数,不等式
取一切实数,不等式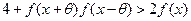 都成立,求
都成立,求 的取值范围.
的取值范围.
(本小题满分13分)
据预测,我国在“十二五”期间内某产品关税与市场供应量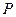 的关系近似地满足:
的关系近似地满足: (其中
(其中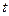 为关税的税率,且
为关税的税率,且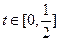 ,
,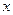 为市场价格,
为市场价格,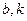 为正常数),当
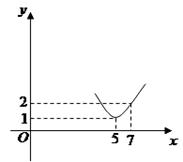
为正常数),当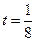 时的市场供应量曲线如图所示;
时的市场供应量曲线如图所示;
(1)根据图象求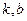 的值;
的值;
(2)若市场需求量为 ,它近似满足
,它近似满足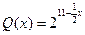 .
.
当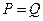 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率
时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率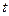 的最小值.
的最小值.