(14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
已知函数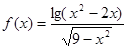 的定义域为
的定义域为 ,
,
(1)求 ;
;
(2)若 ,且
,且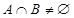 ,求实数
,求实数 的取值范围.
的取值范围.
若函数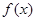 为定义域
为定义域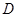 上的单调函数,且存在区间
上的单调函数,且存在区间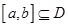 (其中
(其中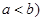 ,使得当
,使得当 时,
时, 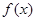 的取值范围恰为
的取值范围恰为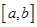 ,则称函数
,则称函数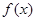 是
是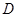 上的正函数,区间
上的正函数,区间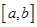 叫做函数的等域区间.
叫做函数的等域区间.
(1)已知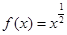 是
是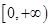 上的正函数,求
上的正函数,求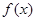 的等域区间;
的等域区间;
(2)试探求是否存在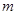 ,使得函数
,使得函数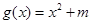 是
是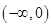 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数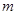 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数 ,恒过定点
,恒过定点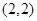 .
.
(1)求实数 ;
;
(2)在(1)的条件下,将函数 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 个单位后得到函数
个单位后得到函数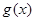 ,设函数
,设函数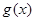 的反函数为
的反函数为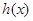 ,直接写出
,直接写出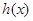 的解析式;
的解析式;
(3)对于定义在 上的函数
上的函数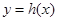 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数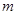 的取值范围.
的取值范围.
一种放射性元素,最初的质量为 ,按每年
,按每年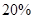 衰减.
衰减.
(1)求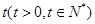 年后,这种放射性元素的质量
年后,这种放射性元素的质量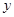 与
与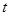 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的 时所经历的时间).(
时所经历的时间).(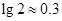 )
)
已知集合 ,集合
,集合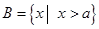 .
.
(1)若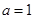 ,求
,求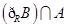 ;
;
(2)若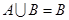 ,求
,求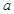 的取值范围.
的取值范围.