求值:
等比数列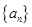 中,
中,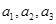 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且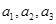 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 |
第二列 |
第三列 |
|
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ) 求数列
求数列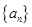 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足: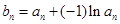 ,求数列
,求数列 的前
的前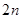 项和
项和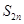 .
.
在 ABC中
ABC中 ,内角A,B,C的对边分别为a,b,c.已知
,内角A,B,C的对边分别为a,b,c.已知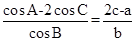 .
.
(I)求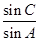 的值;
的值;
(II)若cosB=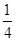 ,
,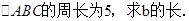
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(I)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(II)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
在某社区举办的“2010亚运知识有奖问答比赛”中,甲、乙、丙三人同时回答一道有关亚运知识的问题,已知甲回答这道题对的概率为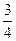 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是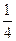 ;
;
(1)求乙、丙两人各自回答这道题对的概率;
(2)用 表示回答该题对的人数,求
表示回答该题对的人数,求 的分布列和
的分布列和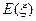 .
.
在直角坐标系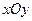 中,以原点
中,以原点 为极点,以
为极点,以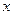 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线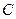 的极坐标方程为
的极坐标方程为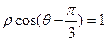 ,
,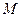 、
、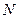 分别为
分别为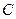 与
与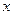 轴,
轴,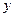 轴的交点,
轴的交点,
(1)写出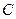 的直角坐标方程,并求
的直角坐标方程,并求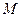 、
、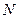 的极坐标;
的极坐标;
(2)设 的中点为
的中点为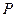 ,求直
,求直 线
线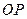 的极坐标方程.
的极坐标方程.