已知函数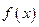 =
=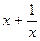 .
.
(1)判断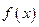 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断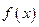 在
在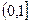 上的单调性并加以证明.
上的单调性并加以证明.
设向量a=(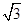 sinx,sinx),b=(cosx,sinx),x∈
sinx,sinx),b=(cosx,sinx),x∈ .
.
(1)若|a|=|b|.求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.
(1)求证:(a-b)⊥c;
(2)若|ka+b+c|>1(k∈R),求k的取值范围.
已知a=(3,4),b=(4,3),求x、y的值使(xa+yb)⊥a,且|xa+yb|=1.
已知向量a= ,b=(
,b=(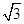 sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b.
(1)求f(x)的最小正周期.
(2)求f(x)在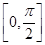 上的最大值和最小值.
上的最大值和最小值.