设函数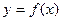 是定义域在
是定义域在 ,并且满足
,并且满足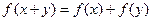 ,
, ,且当
,且当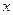 >0时,
>0时, >0。
>0。
(1)求 的值,
的值,
(2)判断函数的奇偶性,
(3)如果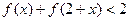 ,求
,求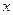 的取值范围。
的取值范围。
(本小题13分)某工厂要建造一个无盖长方体水池,底面一边长固定为8 ,最大装水量为72
,最大装水量为72 ,池底和池壁的造价分别为
,池底和池壁的造价分别为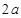 元
元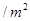 、
、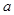 元
元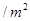 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
(本小题13分)若不等式 的解集是
的解集是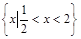 ,求不等式
,求不等式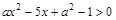 的解集.
的解集.
(本小题12分)在等比数列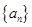 中,
中,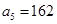 ,公比
,公比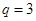 ,前
,前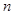 项和
项和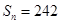 ,求首项
,求首项 和项数
和项数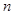 .
.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数 (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
.
(1)求 、
、 的值;
的值;
(2)若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若 有三个不同的实数解,求实数
有三个不同的实数解,求实数
 的取值范围.
的取值范围.
定义 ,
, ,…,
,…, 的“倒平均数”为
的“倒平均数”为 (
( ).已知数列
).已知数列 前
前 项的“倒平均数”为
项的“倒平均数”为 ,记
,记 (
( ).
).
(1)比较 与
与 的大小;
的大小;
(2)设函数 ,对(1)中的数列
,对(1)中的数列 ,是否存在实数
,是否存在实数 ,使得当
,使得当 时,
时, 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(3)设数列 满足
满足 ,
, (
( 且
且 ),
), (
( 且
且 ),且
),且 是周期为
是周期为 的周期数列,设
的周期数列,设 为
为 前
前 项的“倒平
项的“倒平 均数”,求
均数”,求 .
.