某建材商场国庆期间搞促销活动，规定：顾客购物总金额不超过800元，不享受任何折扣，如果顾客购物总金额超过800元，超过800元部分享受一定的折扣优惠，按下表折扣分别累计计算：
| 可以享受折扣优惠金额 |
折扣率 |
| 不超过500元的部分 |
5 ℅ |
| 超过500元的部分 |
10 ℅ |
某人在此商场购物总金额为x元，可以获得的折扣金额为y元.
（1）写出y关于x的解析式. (2) 若y=30，求此人购物实际所付金额。
如图所示，在△ABO中，
=
,
=
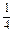
,AD与BC相交于点M，设=a，=b.试用a和b表示向量
.
设两个非零向量a与b不共线，
（1）若
=a+b,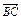
=2a+8b,
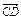=3(a-b)，求证：A、B、D三点共线；
（2）试确定实数k，使ka+b和a+kb共线.
如图所示，若四边形ABCD是一个等腰梯形，AB∥DC，M、N分别是DC、AB的中点，已知
=a，
=b，
=c，试用a、b、c表示
，
，
+
.
定理：若函数
在闭区间[m，n]上是连续的单调函数，且
，则存在唯一一个
。已知
（1）若
是减函数，求a的取值范围。
（2）是否存在
同时成立，若存在，指出c、d之间的等式关系，若不存在，请说明理由。
已知函数
时取最大值2。
是集合
中的任意两个元素，
的最小值为
。
（1）求a、b的值；
（2）若
的值。