(本题满分14分)
已知钝角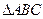 中,角
中,角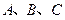 的对边分别为
的对边分别为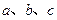 ,且有
,且有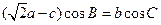
(1)求角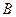 的大小;
的大小;
(2)设向量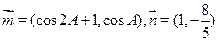 ,且
,且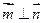 ,求
,求 的值
的值
已知函数f(x)= x3-
x3- x2+x+b,其中a,b∈R.
x2+x+b,其中a,b∈R.
(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=5x-4,求函数f(x)的解析式.
(2)当a>0时,讨论函数f(x)的单调性.
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直线m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由.
已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程.
(2)如果曲线y=f(x)的某一切线与直线y=- x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
已知曲线y= x3+
x3+ ,
,
(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
求下列各函数的导数:
(1)y=(x+1)(x+2)(x+3).
(2)y=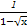 +
+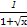 .
.
(3)y=e-xsin2x.