(本题满分12分)若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 接近
接近 .
.
(1)若 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 接近
接近 ;
;
(3)已知函数 的定义域
的定义域 .任取
.任取 ,
, 等于
等于 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
(本小题12分)已知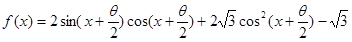
(Ⅰ)若 ,求
,求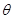 使函数
使函数 为偶函数。
为偶函数。
(Ⅱ)在(I)成立的条件下,求满足 =1,
=1,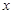 ∈[-π,π]的
∈[-π,π]的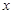 的集合。
的集合。
(本小题满分14分)已知中心在坐标原点O,焦点在 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
(Ⅰ)求椭圆的方程;
(Ⅱ)直线 平行于
平行于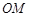 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.
(ⅰ)若 为钝角,求直线
为钝角,求直线 在
在 轴上的截距m的取值范围;
轴上的截距m的取值范围;
(ⅱ)求证直线MA、MB与x轴围成的三角形总是等腰三角形.
(本小题13分)已知 .
.
(I)求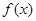 的单调增区间;
的单调增区间;
(II)若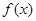 在定义域R内单调递增,求
在定义域R内单调递增,求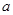 的取值范围;
的取值范围;
(III)是否存在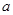 ,使
,使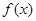 在(-∞,0]上单调递减,在[0,+∞)上单调递增?若存在,求出
在(-∞,0]上单调递减,在[0,+∞)上单调递增?若存在,求出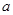 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)已知数列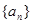 的前n项和
的前n项和 满足
满足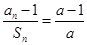 (
(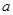 >0,且
>0,且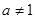 )。数列
)。数列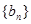 满足
满足
(I)求数列 的通项。
的通项。
(II)若对一切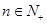 都有
都有 ,求
,求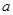 的取值范围。
的取值范围。
(本小题满分12分)在直三棱柱(侧棱垂直底面)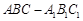 中,
中, ,
,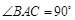 ,且异面直线
,且异面直线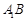 与
与 所成的角等于
所成的角等于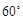 .
.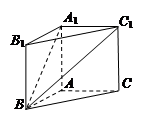
(Ⅰ)求棱柱的高;
(Ⅱ)求 与平面
与平面 所成的角的大小.
所成的角的大小.