若有穷数列 (
( 是正整数),满足
是正整数),满足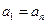 ,
, ,
, ,
,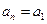 ,即
,即 (
( 是正整数,且
是正整数,且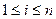 ),就称该数列为“对称数列”.
),就称该数列为“对称数列”.
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且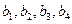 成等差数列,
成等差数列, ,试写出
,试写出 的每一项.
的每一项.
(2)已知 是项数为
是项数为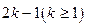 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和 .
.
已知函数f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1.
(Ⅰ)若函数f(x)在x=-2处有极值,求f(x)的表达式;
(Ⅱ)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围.
如图,在五面体ABCDEF中,FA  平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=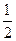 AD
AD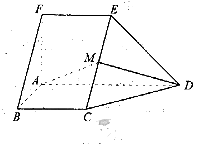
(1)证明平面AMD 平面CDE;
平面CDE;
(2)求二面角A-CD-E的余弦值
已知
的角
、
、
所对的边分别是
、
、
,设向量
,
,
.
(1)若
,求证:
为等腰三角形;
(2)若
,边长
,角
,求
的面积.
设函数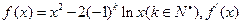 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{ }满足
}满足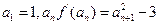 .证明:数列{
.证明:数列{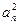 }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有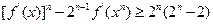 成立.
成立.
已知双曲线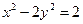 的左、右两个焦点为
的左、右两个焦点为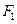 ,
,  ,动点P满
,动点P满
足|P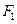 |+| P
|+| P |=4.
|=4.
(I)求动点P的轨迹E的方程;
(1I)设过 且不垂直于坐标轴的动直线l交轨迹E于A、B两点,问:终段O
且不垂直于坐标轴的动直线l交轨迹E于A、B两点,问:终段O
上是否存在一点D,使得以DA、DB为邻边的平行四边形为菱形?作出判断并证明.