已知函数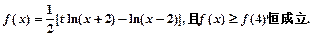
(1)求t的值;
(2)求x为何值时,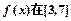 上取得最大值;
上取得最大值;
(3)设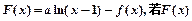 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.
假设甲乙两种品牌的同类产品在某地区市场上销售量相等,为了解他们的使用寿命,现从两种品牌的产品中分别随机抽取100个进行测试,结果统计如下:
(Ⅰ)估计甲品牌产品寿命小于200小时的概率;
(Ⅱ)这两种品牌产品中,某个产品已使用了200小时,试估计该产品是甲品牌的概率.
直三棱柱
中,
.
(Ⅰ)证明
;
(Ⅱ)已知
,求三棱锥
的体积.
函数
的最大值为3, 其图像相邻两条对称轴之间的距离为
,
(1)求函数
的解析式;
(2)设
,则
,求
的值
已知等比数列
的公比为
.
(1)若
= ,求数列
的前
项和;
,求数列
的前
项和;
(Ⅱ)证明:对任意
,
,
,
成等差数列.
已知
为正实数,
为自然数,抛物线
与
轴正半轴相交于点
,设
为该抛物线在点
处的切线在
轴上的截距.
(1)用
和
表示
;
(2)求对所有
都有
成立的
的最小值;
(3)当
时,比较
与
的大小,并说明理由.