已知 ,
, , 且
, 且 ,
, , 求
, 求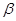 的值.
的值.
如图△ABC内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D.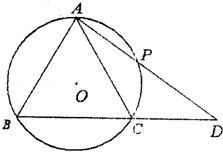
(Ⅰ)求证:AC2=AP•AD;
(Ⅱ)若∠ABC=60°,⊙O的半径为1,且P为弧AC的中点,求AD的长.
已知函数f(x)=ln(x+1),g(x)=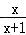 .
.
(1)求h(x)=f(x)﹣g(x)的单调区间;
(2)求证:f2(x)≤xg(x).
数列{an}满足a1=2,an+1=an2+6an+6(n∈N×)
(Ⅰ)设Cn=log5(an+3),求证{Cn}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设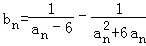 ,数列{bn}的前n项的和为Tn,求证:
,数列{bn}的前n项的和为Tn,求证: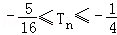 .
.
如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.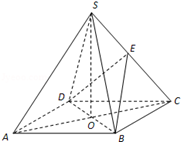
(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC;
(Ⅲ)(理科)当二面角E﹣BD﹣C的大小为45°时,试判断点E在SC上的位置,并说明理由.
已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M且有|PM|=|PO|(O为原点),求使|PM|取得最小值时点P的坐标.