如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.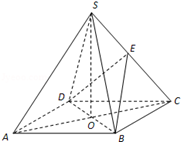
(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC;
(Ⅲ)(理科)当二面角E﹣BD﹣C的大小为45°时,试判断点E在SC上的位置,并说明理由.
(本小题满分12分)某汽车厂生产A、B两类轿车,每类轿车均有舒适型和标准型两种,某月的产量如下表:
按分层抽样的方法在该月生产的轿车中抽取50辆,其中A类轿车20辆。
(I)求x的值;
(II)用分层抽样的方法在B类轿车中抽取一个容量为6的样本,从样本中任意取2辆,求至少有一辆舒适轿车的概率。
(本小题满分12分)已知函数 =
= 在
在 处取得极值.
处取得极值.
(1)求实数 的值;
的值;
(2) 若关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3) 证明: .参考数据:
.参考数据:
(本小题满分12分)已知离心率为 的椭圆
的椭圆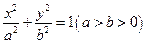 上的点到
上的点到
左焦点 的最长距离为
的最长距离为
(1)求椭圆的方程;
(2)如图,过椭圆的左焦点 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦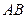 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点” 的坐标.
的坐标.
(本小题满分12分)
已知数列 满足
满足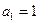 ,且
,且 ,
,
(1)证明数列 是等比数列;
是等比数列;
(2)求数列 的前
的前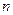 项和
项和 .
.
(本小题满分12分)
如图,已知四棱锥 中,侧棱
中,侧棱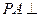 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形, ,
, ,
, ,
, 分别是
分别是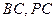 的中点.
的中点.
(1)求证: 平面
平面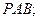
(2)当平面 与底面
与底面 所成二面角为
所成二面角为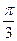 时,求二面角
时,求二面角 的大小.
的大小.