已知命题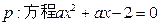 在[-1,1]上有解,命题q:
在[-1,1]上有解,命题q:
只有一个实数x满足: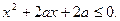
(I)若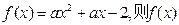 的图象必定过两定点,试
的图象必定过两定点,试 写出这两定点的坐标
写出这两定点的坐标
(只需填写出两点坐标即可);
(II)若命题“p或q”为假命题,求实数a的取值范围.
已知函数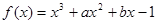 在
在 处有极值
处有极值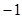 。
。
(Ⅰ)求实数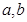 的值;
的值;
(Ⅱ)求函数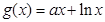 的单调区间。
的单调区间。
一个口袋中装有大小相同的2个白球和3个黑球。
(Ⅰ)从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率。
在平面内,如果用一条直线去截正方形的一个角,那么截下的一个直角三角形按图所标边长,由勾股定理有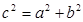 。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥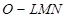 ,如果用
,如果用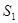 ,
,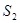 ,
,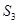 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么你类比得到的结论是。
表示截面面积,那么你类比得到的结论是。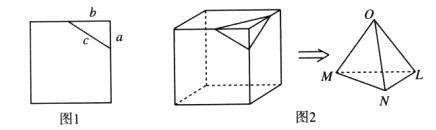
在数列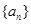 中,对于任意
中,对于任意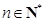 ,等式
,等式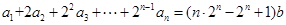 成立,其中常数
成立,其中常数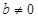 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证:数列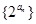 为等比数列;
为等比数列;
(Ⅲ)如果关于n的不等式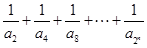
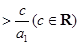 的解集为
的解集为 ,求b和c的取值范围.
,求b和c的取值范围.
设函数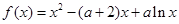 ,其中
,其中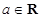 .
.
(Ⅰ)若函数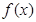 的图象在点
的图象在点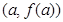 处的切线与直线
处的切线与直线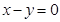 平行,求实数
平行,求实数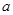 的值;
的值;
(Ⅱ)求函数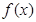 的极值.
的极值.