如图△ABC内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D.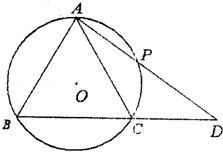
(Ⅰ)求证:AC2=AP•AD;
(Ⅱ)若∠ABC=60°,⊙O的半径为1,且P为弧AC的中点,求AD的长.
在可行域内任取一点,规则如流程图所示,求输出数对(x,y)的概率.
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(≥73公斤)的职工,求体重为76公斤的职工被抽取到的概率.
某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的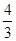 倍.
倍.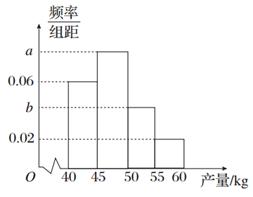
(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树中随机抽取2株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间的产品较稳定.
某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,但可见部分如图,据此解答下列问题:
(1)求分数在[50,60]的频率及全班人数;
(2)求分数在[80,90]之间的频数,并计算频率分布直方图中[80,90]间的矩形的高.