(本小题满分12分)某企业2005年的利润为500万元,因设备老化等原因,若不进行技术改造,预计企业利润将从2006年开始每年减少20万元。为此企业在2006年一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第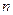 年利润为
年利润为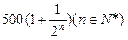 万元。
万元。
(1)若不进行技术改造,则从2006年起的前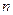 年的利润共
年的利润共 万元;若进行技术改造后,则从2006年起的前
万元;若进行技术改造后,则从2006年起的前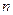 年的纯利润(扣除技术改造600万元资金)共
年的纯利润(扣除技术改造600万元资金)共 万元,分别求
万元,分别求 ;
;
(2)依据预测,从2006年起至少经过多少年技术改造后的纯利润超过不改造的利润?
(本小题满分14分)已知函数 的图像经过点
的图像经过点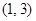 ,并且
,并且 是偶函数.
是偶函数.
(1)求实数 、
、 的值;
的值;
(2)用定义证明:函数 在区间
在区间 上是增函数.
上是增函数.
(本小题满分14分)东华旅行社为某旅游团包飞机去旅游,其中旅行社的包机费为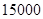 元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在
元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在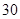 人或
人或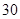 人以下,飞机票每张收费
人以下,飞机票每张收费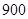 元;若旅游团的人数多于
元;若旅游团的人数多于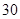 人,则给予优惠,每多
人,则给予优惠,每多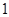 人,机票费每张减少
人,机票费每张减少 元,但旅游团的人数最多有
元,但旅游团的人数最多有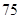 人,设旅游团的人数为
人,设旅游团的人数为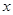 人,每张飞机票价为
人,每张飞机票价为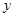 元,旅行社可获得的利润为
元,旅行社可获得的利润为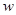 元.
元.
(1)写出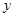 与
与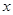 的函数关系式;
的函数关系式;
(2)写出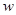 与
与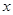 的函数关系式;
的函数关系式;
(3)那么旅游团的人数为多少时,旅行社可获得的利润最大?
(本小题满分14分)已知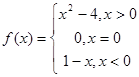
(1)求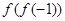 ,
,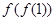 ;
;
(2)画出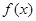 的图像;
的图像;
(3)若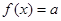 ,问
,问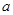 为何值时,方程没有根?有一个根?两个根?
为何值时,方程没有根?有一个根?两个根?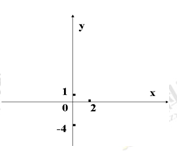
(本小题满分12分)
(1)
(2)
(本小题满分12分)已知全集 ,集合
,集合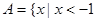 或
或 ,
,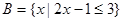 .
.
求:(1)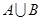 (2)
(2)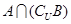 (3)
(3)  .
.