设函数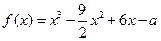 .
.
(Ⅰ) 对于任意实数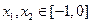 ,求证:
,求证: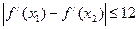 ;
;
(Ⅱ) 若方程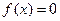 有且仅有三个实根,求
有且仅有三个实根,求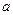 的取值范围.
的取值范围.
以下茎叶图记录了甲组3名同学寒假假期中去图书馆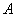 学习的次数和乙组4名同学寒假假期中去图书馆
学习的次数和乙组4名同学寒假假期中去图书馆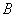 学习的次数. 乙组记录中有一个数据模糊,无法确认,在图中以x表示.
学习的次数. 乙组记录中有一个数据模糊,无法确认,在图中以x表示.
(1)如果x =7,求乙组同学去图书馆学习次数的平均数和方差;
(2)如果x =9,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.
在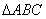 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为 且
且 ,b=2,求A的值。
,b=2,求A的值。
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为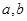 .
.
(1)求直线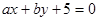 与圆
与圆 相切的概率;
相切的概率;
(2)将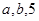 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
“H7N9禽流感”问题越来越引起社会关注,我校对高一600名学生进行了一次“H7N9禽流感”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
已知 ,
,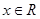 .
.
(1)求函数 的最小正周期及对称中心;
的最小正周期及对称中心;
(2)求函数的单调递减区间.