(本小题满分14分)
已知:数列{ }的前n项和为
}的前n项和为 ,满足
,满足 =
=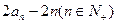
(Ⅰ)证明数列{ }是等比数列.并求数列{
}是等比数列.并求数列{ }的通项公式
}的通项公式 =?
=?
(Ⅱ)若数列{ }满足
}满足 =log2(
=log2( ),而
),而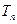 为数列
为数列 的前n项和,求
的前n项和,求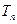 =?
=?
设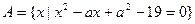 ,
, ,
,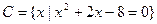 .
.
①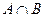 =
=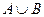 ,求a的值;
,求a的值;
②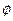

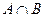 ,且
,且 =
=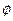 ,求a的值;
,求a的值;
③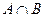 =
=

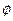 ,求a的值;
,求a的值;
数集A满足条件:若 ,则
,则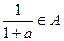 .
.
①若2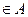 ,则在A中还有两个元素是什么;
,则在A中还有两个元素是什么;
②若A为单元集,求出A和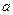 .
.
设函数 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有 且当
且当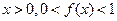
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减。
若二次函数满足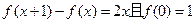 。
。
(1) 求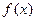 的解析式;
的解析式;
(2) 若在区间[-1,1]上不等式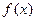 >2x+m恒成立,求实数m的取值范围。
>2x+m恒成立,求实数m的取值范围。
我们为了探究函数 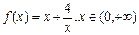 的部分性质,先列表如下:
的部分性质,先列表如下:
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
请你观察表中y值随x值变化的特点,完成以下的问题.
首先比较容易的看出来:此函数在区间(0,2)上是递减的;
(1)函数 在区间上递增.
在区间上递增.
当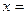 时,
时, .
.
(2)请你根据上面性质作出此函数的大概图像; (3)证明:此函数在区间上(0,2)是递减的.
(3)证明:此函数在区间上(0,2)是递减的.