(本题满分14分,每小题各7分)计算下列各式
(Ⅰ)
(Ⅱ) 
.已知抛物线 的准线为
的准线为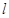 ,焦点为F,
,焦点为F,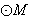 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与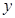 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为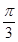 的直线
的直线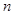 ,交
,交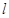 于点A,交
于点A,交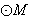 于另一点B,且AO=OB=2.
于另一点B,且AO=OB=2.
(1)求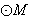 和抛物线C的方程;
和抛物线C的方程;
(2)若P为抛物线C上的动点,求 的最小值;
的最小值;
(3)过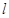 上的动点Q向
上的动点Q向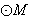 作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
设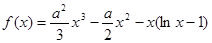 .
.
(1) 当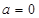 时,求
时,求 的单调区间.
的单调区间.
(2)当 时,讨论
时,讨论 的极值点个数。
的极值点个数。
.如图(1),在直角梯形ABCD中,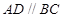 ,
,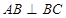 ,
,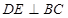 ,
, ,
, ,以DE为轴旋转至图(2)位置,F为DC的中点.
,以DE为轴旋转至图(2)位置,F为DC的中点.
(1)求证: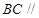 平面
平面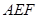
(2)若平面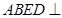 平面
平面 ,且BC垂直于AE
,且BC垂直于AE
求①二面角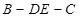 的大小.
的大小.
②直线BF与平面ABED所成角的正弦值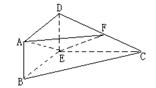

已知等比数列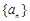 中,
中, .记数列
.记数列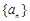 的前n项和为
的前n项和为 .
.
(1)求数列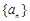 的通项公式;
的通项公式;
(2)数列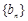 中,
中,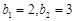 ,数列
,数列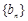 的前n项和
的前n项和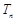 满足:
满足: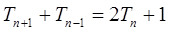 ,
, , 求:
, 求: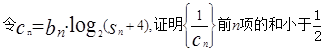 .
.
在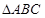 中,角
中,角 的对边分别为
的对边分别为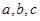 .已知
.已知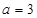 ,
,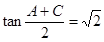 .
.
(1)求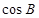 的值.
的值.
(2)求 的取值范围.
的取值范围.