(本题10分)某家公司每月生产两种布料A和B,所有原料是两种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量。
| 羊毛颜色 |
每匹需要( kg) |
供应量(kg) |
|
| 布料A |
布料B |
||
| 红 |
4 |
4 |
1400 |
| 绿 |
6 |
3 |
1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最大的利润是多少?
(本小题满分12 分)
已知函数f(x)= 的定义域为R,且
的定义域为R,且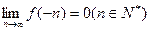 ;
;
(1)求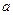 与
与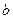 的取值范围;
的取值范围;
(2)若f(1)= ,且f(x)在[0,1]上的最小值为,求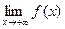 的值。
的值。
(本小题满分12 分)
已知函数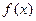 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的 、
、 ∈R,都满足
∈R,都满足 ,若
,若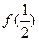 =1,
=1,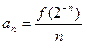 ;
;
(1)求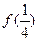 、
、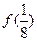 、
、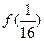 的值;
的值;
(2)猜测数列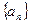 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
(本小题满分12分)
设f(x)是定义在[-1,1]上的奇函数,对于任意的
 当
当 时,都
时,都
有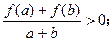
(1)若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集,求c的取值范围;
(2)判断函数f(x)在[-1,1]上的单调性,并用定义证明。
(本小题满分12分)
已知p: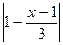 ≤2, q:
≤2, q: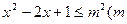 >0)
>0)
若非p是非q的必要不充分条件,求实数m的取值范围。
(本小题满分10 分)
解关于x的不等式: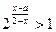 (
(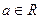 )。
)。