《选修4-4:坐标系与参数方程》已知直线L的参数方程: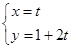 (t为参数)和圆C的极坐标方程:
(t为参数)和圆C的极坐标方程: 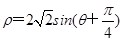 (θ为参数).
(θ为参数).
(1)求圆C的直角坐标方程.
(2)判断直线L和圆C的位置关系.
在平面直角坐标系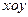 中,如图,已知椭圆
中,如图,已知椭圆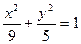 的左右顶点为A,B,右焦点为F,设过点T(
的左右顶点为A,B,右焦点为F,设过点T(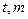 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
, ,其中m>0,
,其中m>0,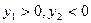
①设动点P满足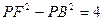 ,求点P的轨迹
,求点P的轨迹
②设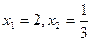 ,求点T的坐标
,求点T的坐标
③设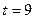 ,求证:直线MN必过x轴上的一定点(其坐标与m无关)
,求证:直线MN必过x轴上的一定点(其坐标与m无关)
 |
某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β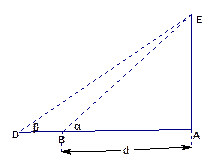
(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离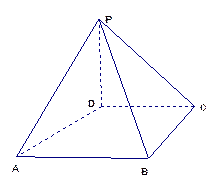
在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1)
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长
(2)设实数t满足(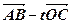 )·
)·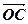 =0,求t的值
=0,求t的值
已知集合 ,对于 ,定义 与 的差为 ; 与 之间的距离为 ,
(Ⅰ)当 时,设 , ,求 , ;
(Ⅱ)证明: ,有 ,且 ;
(Ⅲ)证明: , 三个数中至少有一个是偶数.