设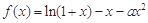 .
.
(1) 当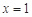 时,
时,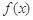 取到极值,求
取到极值,求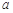 的值;
的值;
(2)当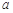 满足什么条件时,
满足什么条件时,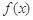 在区间
在区间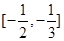 上有单调递增区间?
上有单调递增区间?
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
在△ABC中,BC=a,AC=b,a,b是方程 的两个根,且
的两个根,且 。
。
求:(1)角C的度数; (2)AB的长度。
已知 是等差数列,其中
是等差数列,其中
(1)求 的通项公式
的通项公式
(2)数列 从哪一项开始小于0;
从哪一项开始小于0;
(3)求 值。
值。
已知命题p:关于x的方程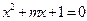 有两个不相等的负根. 命题q:关于x的方程
有两个不相等的负根. 命题q:关于x的方程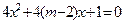 无实根,若
无实根,若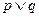 为真,
为真,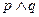 为假,求
为假,求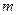 的取值范围.
的取值范围.
a,b,c为△ABC的三边,其面积 =12
=12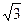 ,bc=48,b-c=2,求a.
,bc=48,b-c=2,求a.