某商场经营一批进价是每件30元的商品, 在市场销售中发现此商品的销售单
在市场销售中发现此商品的销售单
价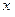 元与日销售量
元与日销售量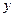 件之间有如下关系:
件之间有如下关系:
销 售单价 售单价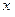 (元) (元) |
30 |
40 |
45 |
50 |
日销售量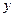 (件) (件) |
60 |
30 |
15 |
0 |
(1) 在所给坐标系 中,根据表中提
中,根据表中提 供的数据描出实数对
供的数据描出实数对 对应的点,并确定
对应的点,并确定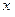 与
与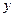 的一个函数关系式
的一个函数关系式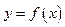 ;
;
(2)设经营此商品的日销售利润为 元,根据上述关系式写出
元,根据上述关系式写出 关于
关于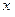 的函数关系式,并指出销售单价
的函数关系式,并指出销售单价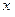 为多少时,才能获得最大日销售利润。
为多少时,才能获得最大日销售利润。