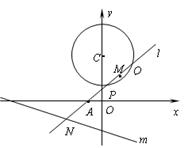
已知过点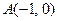 的动直线
的动直线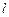 与圆
与圆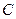 :
: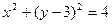 相交于
相交于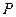 、
、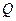 两点,
两点,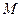 是
是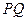 中点,
中点,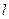 与直线
与直线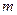 :
: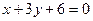 相交于
相交于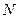 .
.
(1)当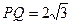 时,求直线
时,求直线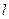 的方程;
的方程;
(2)探索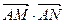 是否与直线
是否与直线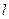 的倾斜角有关,
的倾斜角有关,
若无关,请求出其值;若有关,请说明理由..
淮南八公山某种豆腐食品是经过A、B、C三道工序加工而成的,A、B、C工序的产品合格率分别为 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
(Ⅰ)正式生产前先试生产2袋食品,求这2袋食品都为废品的概率;
(Ⅱ)设ξ为加工工序中产品合格的次数,求ξ的分布列和数学期望.
如图,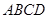 是边长为3的正方形,
是边长为3的正方形,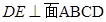 ,
, ,
, 与平面
与平面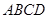 所成的角为
所成的角为 .
.
(1)求二面角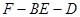 的的余弦值;
的的余弦值;
(2)设点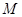 是线段
是线段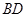 上一动点,试确定
上一动点,试确定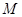 的位置,使得
的位置,使得 ,并证明你的结论.
,并证明你的结论.
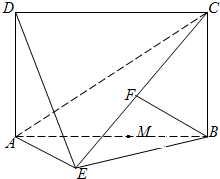
如图,四边形 为矩形,
为矩形,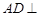 平面
平面 ,
, 为
为 上的点,且
上的点,且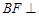 平面
平面 .
. 
(1)求三棱锥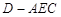 的体积;
的体积;
(2)设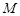 在线段
在线段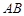 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点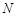 ,使得
,使得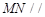 平面
平面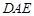 .
.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=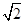 .
.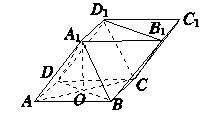
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).
(1)按照画三视图的要求画出该多面体的俯视图;
(2)在所给直观图中连接BC′,求证:BC′∥面EFG.