已知数列
,满足条件:
,n∈N﹡.
(Ⅰ)求证:数列{
+1}为等比数列;
(Ⅱ)令
,
是数列{
}的前n项和,证明
.
(本小题满分12分)
已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)试探究在DE上是否存在点Q,使得AQ BQ并说明理由.
BQ并说明理由.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.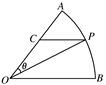
(本小题满分12分)
设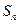 为数列{
为数列{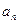 }的前n项和,
}的前n项和,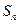 =kn2+n,n∈N*,其中k是常数.
=kn2+n,n∈N*,其中k是常数.
(1)求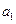 及
及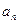 ;
;
(2)若对于任意的m∈N*, ,
, ,
, 成等比数列,求k的值.
成等比数列,求k的值.
(本小题满分10分)
已知 :方程
:方程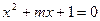 有两个不等的负实根,
有两个不等的负实根,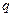 :方程
:方程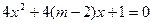 无实根. 若
无实根. 若 或
或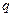 为真,
为真, 且
且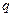 为假. 求实数
为假. 求实数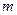 的取值范围。
的取值范围。
已知数列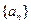 中
中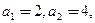 数列
数列 满足:
满足:
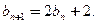
(1)求证 数列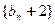 是等比数列(要指出首项与公比)
是等比数列(要指出首项与公比)
(2)求数列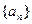 的通项公式.
的通项公式.