(本小题满分12分)
在△ 中,角A、B、C所对的边分别为a,b,c,已知
中,角A、B、C所对的边分别为a,b,c,已知 ,其中C为锐角.
,其中C为锐角.
(Ⅰ)求 的值;
的值;
(Ⅱ)当 时,求b及c的值.
时,求b及c的值.
已知a,b,c分别是 的三个内角A,B,C的对边,
的三个内角A,B,C的对边,
(1)求A的大小;
(2)当 时,求
时,求 的取值范围.
的取值范围.
已知等差数列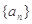 中,公差
中,公差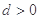 ,其前
,其前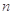 项和为
项和为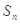 ,且满足:
,且满足: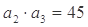 ,
, .
.
(1)求数列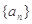 的通项公式;
的通项公式;
(2)令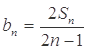 ,
,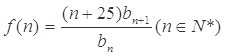 ,求
,求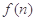 的最小值.
的最小值.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形,且侧面AA1C1C是边长为2的正方形,E是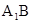 的中点,F在棱CC1上。
的中点,F在棱CC1上。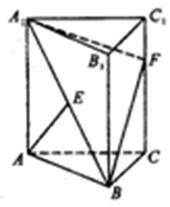
(1)当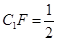 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积;
(2)当点F使得A1F+BF最小时,判断直线AE与A1F是否垂直,并证明的结论。
如图,在直角坐标系中,射线OA: x-y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.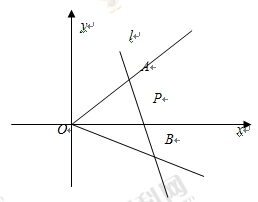
(1)当AB中点为P时,求直线AB的斜率
(2)当AB中点在直线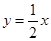 上时,求直线AB的方程.
上时,求直线AB的方程.
如图在正三棱锥P-ABC中,侧棱长为3,底面边长为2,E为BC的中点,
(1)求证:BC⊥PA
(2)求点C到平面PAB的距离