(本小题满分12分)
如图,在直三棱柱 中,
中, .
. 
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证: .
.
(本小题满分14分)先后抛掷一枚骰子两次,将得到的点数分别记为 ,
, 。
。
(1)求 的概率;
的概率;
(2)求点 在函数
在函数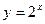 图像上的概率;
图像上的概率;
(3)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
(本小题满分14分)已知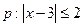 ,
, ,
,
若 p是
p是 q充分而不必要条件,求实数m的取值范围
q充分而不必要条件,求实数m的取值范围
(本小题满分14分)
一直线过点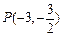 ,被圆
,被圆 截得的弦长为8, 求此弦所在直线方程.
截得的弦长为8, 求此弦所在直线方程.
(本小题满分12分)双曲线与椭圆 有相同焦点,且经过点
有相同焦点,且经过点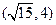 .
.
(1)求双曲线的方程;
(2)求双曲线的离心率.
(本小题满分12分)为了检测某种产品的质量,抽取了一个容量为40的样本,检
测结果为一等品8件,二等品18件,三等品12件,次品2件.
(1)列出样本的频率分布表;
(2)画出表示样本频率分布的条形图;
(3)根据上述结果,估计此种新产品为二等品或三等品的概率是多少?