如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的木箱A放在木板B上。一根轻绳一端拴在木箱上，另一端拴在地面的木桩上，绳绷紧时与水
平面的夹角为θ=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4。重力加速
度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出，试求：（sin37°=0.6，cos37°=0.8）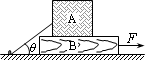
（1）绳上张力T的大小；
（2）拉力F的大小。
如图，竖直固定轨道abcd段光滑，长为L=1．0m的平台de段粗糙，abc段是以O为圆心的圆弧．小球A和B紧靠一起静止于e处，B的质量是A的4倍．两小球在内力作用下突然分离，A分离后向左始终沿轨道运动, 与de段的动摩擦因数μ=0．2，到b点时轨道对A的支持力等于A的重力的
, B分离后平抛落到f点，f到平台边缘的水平距离S= 0．4m,平台高h=0．8m，g取10m/s2，求：
（1）AB分离时B的速度大小vB；
（2）A到达d点时的速度大小vd；
（3）圆弧 abc的半径R．
(16分)如图所示，一圆环A套在一粗细均匀的圆木棒B上，圆环A的高度相对B的长度可以忽略不计．A和B的质量都是0.5kg，A和B之间的滑动摩擦力为3N．开始时B竖直放置，下端离地面高度
，A在B的顶端．现让它们由静止开始自由下落，当木棒与地面相碰后，木棒以竖直向上的速度反向运动．设碰撞时间很短，碰撞无机械能损失，不考虑空气阻力，取当地的重力加速度g取l0m/s2．试求：
（1）木棒第一次着地时速度的大小；
（2）A与地第一次碰撞后上升的最大高度；
（3）A上升至最大高度时，B的速度的大小；
（4）若在棒第二次着地前，要使A不脱离棒，棒的最小长度是多少？
(10分)汽车在高速公路上行驶的最高速度规定不超过120km/h, 发生故障时，警告标志应标明在故障车来车方向150m以外．某校研究性学习小组根据调查收集得到下面的资料，想通过探究性学习来说明“发生故障时警告标志应标明在故障车来车方向150m以外”的理论依据是否科学，假如你是小组成员之一，请你分析说明．（g取l0m/s2）
资料一：驾驶员的反应时间(从发现情况，经操纵刹车到车开始减速所经历的时间): 0.3s～0.6s之间
资料二：各种路面与轮胎之间的动摩擦因数：
| 路面 |
动摩擦因数 |
| 干沥青与混凝土路面 |
0.7～0.8 |
| 干碎石路面 |
0.6～0.7 |
| 湿沥青与混凝土路面 |
0.4～0.5 |
(8分)一重为G的小球，套于竖直放置的半径为R的光滑大圆环上，一劲度系数为k，自然长度为
的轻质弹簧，其上端固定在大圆环的最高点，下端与小球相连，如图所示，不考虑一切摩擦。求小球静止时弹簧与竖直方向的夹角。
(8分)一机动车拉一拖车，由静止开始在水平轨道上匀加速前进，在运动开始后的头10s内走过40m，然后将拖车解脱．但机车的牵引力仍旧不变，再过10s两车相距60m．试求机动车和拖车质量之比．（计算时一切阻力均不计）