(本小题满分12分)
设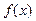 是定义域为
是定义域为 的奇函数,且它在区间
的奇函数,且它在区间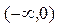 上单调增.
上单调增.
(1)用定义证明: 在
在 上的单调性;
上的单调性;
(2)若 且
且 试判断
试判断 的符号;
的符号;
(3)若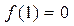 解关于
解关于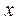 的不等式
的不等式 .
.
(本小题满分16分)设函数f(x)=xsinx(x∈R),
(Ⅰ)证明f(x+2kπ)-f(x)=2kπsinx,其中k为整数;
(Ⅱ)设x0为f(x)的一个极值点,证明  ;
;
(提示 )
)
(Ⅲ)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列a1,a2,,an,,证明 .
.
(本小题满分16分)已知函数 的图像过点
的图像过点 ,且在
,且在 处的切线的斜率为
处的切线的斜率为 ,(
,( 为正整数)
为正整数)
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若数列 满足:
满足: ,
, ,令
,令 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)对于(Ⅱ)中的数列 ,令
,令 ,求数列
,求数列 的前
的前 项的和
项的和 .
.
(本小题满分16分)已知奇函数 的定义域为
的定义域为 ,当
,当 时,
时, .
.
(1)求函数 在
在 上的值域;
上的值域;
(2)若 ,y=
,y= 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
(本小题满分14分)某旅游景点预计2014年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似满足 ,已知第x月的人均消费额q(x)(单位:元)与x的近似关系是 q(x)=
,已知第x月的人均消费额q(x)(单位:元)与x的近似关系是 q(x)=
(1)写出2014年第x月的旅游人数f(x)(单位:万人)与x的函数关系式;
(2)试问2014年哪个月的旅游消费总额最大,最大旅游消费额为多少万元?
(本小题满分14分)设锐角三角形ABC的内角A,B,C的对边分别为 ,
,
(Ⅰ)求B的大小;
(Ⅱ)求 的取值范围
的取值范围