(本题6分)
在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.
(1)试通过计算,比较风筝A与风筝B谁离地面更高?
(2)求风筝A与风筝B的水平距离. (精确到0.01 m;)
某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?
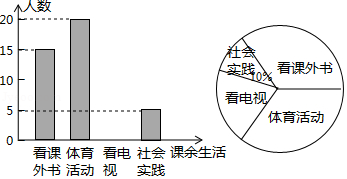
为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求 的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.
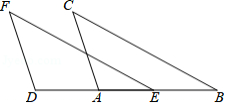
如图, , , .求证: .
已知直线 与 轴、 轴分别相交于 、 两点,抛物线 经过 、 两点,点 在线段 上,从 点出发,向点 以每秒1个单位的速度匀速运动;同时点 在线段 上,从点 出发,向点 以每秒 个单位的速度匀速运动,连接 ,设运动时间为 秒
(1)求抛物线解析式;
(2)当 为何值时, 为直角三角形;
(3)过 作 轴交抛物线于 ,连接 ,是否存在点 使 ,若存在,求出点 的坐标,若不存在,请说明理由.

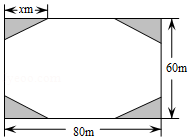
结合西昌市创建文明城市要求,某小区业主委员会决定把一块长 ,宽 的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于 ,不大于 ,预计活动区造价60元 ,绿化区造价50元 ,设绿化区域较长直角边为 .
(1)用含 的代数式表示出口的宽度;
(2)求工程总造价 与 的函数关系式,并直接写出 的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出 为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化 ,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少 .