15分)已知正方体ABCD-A1B1C1D1, O是底ABCD对角线的交点.
求证:(1) //面A1B1D1;
//面A1B1D1;
(2)A1C⊥面AB1D1;
(3)求 。
。
椭圆C: 长轴为8离心率
长轴为8离心率
(1)求椭圆C的标准方程;
(2)过椭圆C内一点M(2,1)引一条弦,使弦被点M平分,
求这条弦所在的直线方程。
一个圆锥高h为 ,侧面展开图是个半圆,求:
,侧面展开图是个半圆,求:
(1)其母线l与底面半径r之比;
(2)锥角 ;
;
(3)圆锥的表面积
(本小题满分14分)
|
|
.如图,ABCD是梯形,AB//CD, ,PA⊥面ABCD,
,PA⊥面ABCD,
|
(Ⅱ)求直线AC与PB所成角的余弦值;
(Ⅲ)在面PAB内能否找一点N,使NE⊥面PAC. 若存在,找出并证明;若不存在,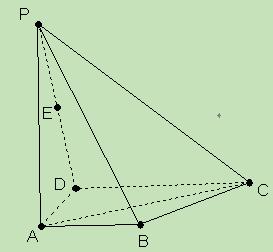
(本小题满分14分)已知在平面直角坐标系xoy中的一个椭圆,它的中心在原
点,左焦
(1)求该椭圆的标准方程;
(2)若P是椭圆上的动点,求线段PA中点M的轨迹方程;
(3)过原点O的直线交椭圆于点B、C,求△ABC面积的最大值。