某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利、尽快减少库存,商场决定采取适当降价措施 . 经调查发现,如果每件衬衫每天降价1元,商场平均每天多售2件.于是商场经理决定每件衬衫降价15元 . 经理的决定正确吗?
(写出详细的说明或计算步骤)
(本小题满分12分)已知抛物线
 的焦点为
的焦点为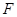 ,抛物线上存在一点
,抛物线上存在一点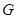 到焦点的距离为
到焦点的距离为 ,且点
,且点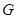 在圆
在圆
 上.
上.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)已知椭圆
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为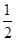 .直线
.直线 交椭圆
交椭圆 于
于 、
、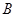 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求 的取值范围.
的取值范围.
(本小题满分12分)如图,四棱锥 中,底面四边形
中,底面四边形 为直角梯形,对角线
为直角梯形,对角线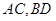 交与点
交与点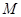 ,
, ,
, 底面
底面 ,点
,点 为棱
为棱 上一动点。
上一动点。
(Ⅰ)证明: ;
;
(Ⅱ)若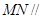 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的
态度进行调查,得到的统计数据如下表所示:
| 积极参加班级工作 |
不积极参加班级工作 |
合计 |
|
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性不高 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(Ⅰ)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系? 请说明理由.
附:
 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |

(本小题满分12分)已知函数f(x)=(sinx+cosx)2+2 sin2x.
sin2x.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2acosC+c=2b,求f(B)的取值范围.
(本小题满分10分)选修4-5:不等式选讲
(1)设 ,且满足:
,且满足: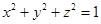 ,
, ,求
,求 的值;
的值;
(2)设不等式 的解集为
的解集为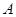 ,且
,且 ,
, .求函数
.求函数 的最小值.
的最小值.