(本小题满分12分)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的
态度进行调查,得到的统计数据如下表所示:
| |
积极参加班级工作 |
不积极参加班级工作 |
合计 |
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性不高 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(Ⅰ)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系? 请说明理由.
附:
 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |

如图,曲线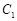 是以原点O为中心、
是以原点O为中心、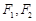 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以O为顶点、
是以O为顶点、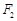 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线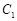 和
和 的交点且
的交点且 为钝角,若
为钝角,若 ,
,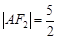 .
.
(Ⅰ)求曲线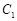 和
和 的方程;
的方程;
(Ⅱ)过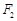 作一条与
作一条与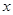 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线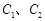 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问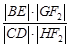 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
已知四边形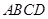 满足
满足 ∥
∥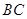 ,
,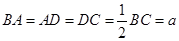 ,
,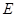 是
是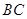 的中点,将
的中点,将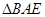 沿着
沿着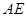 翻折成
翻折成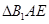 ,使面
,使面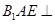 面
面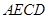 ,
,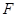 为
为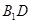 的中点.
的中点. 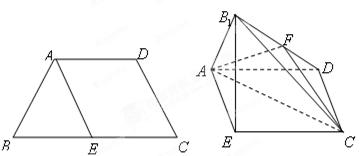
(Ⅰ)求四棱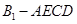 的体积;
的体积;
(Ⅱ)证明: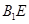 ∥面
∥面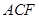 ;
;
(Ⅲ)求面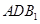 与面
与面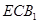 所成二面角的余弦值.
所成二面角的余弦值.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如右图).记成绩不低于90分者为“成绩优秀”.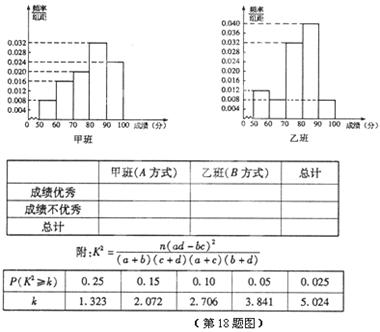
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为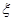 ,求
,求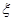 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面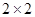 列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
已知各项都是正数的等比数列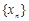 ,满足
,满足
(I)证明数列 是等差数列;
是等差数列;
(II)若 ,当
,当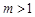 时, 不等式
时, 不等式 对
对 的正整数恒成立,求
的正整数恒成立,求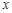 的取值范围.
的取值范围.
已知函数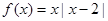
(1)写出 的单调区间
的单调区间
(2)解不等式
(3)设 上的最大值
上的最大值