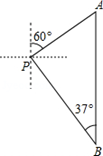
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.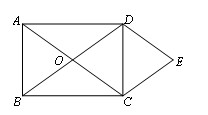
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
如图,一抛物线经过点A(−2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.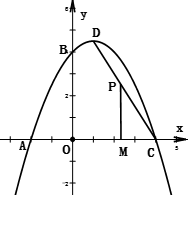
(1)求该抛物线的函数关系式及顶点D坐标.
(2)如图,若P为线段CD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAB的面积的最大值和此时点P的坐标.
(3)过抛物线顶点D,作DE⊥x轴于E点,F(m,0)是x轴上一动点,若以BF为直径的圆与线段DE有公共点,求m的取值范围.
如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.
(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.
某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=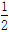 x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
(1)试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)请问在这30天的销售期中,哪一天的日销售利润最大?并求出这个最大利润值.
(注:销售利润=销售收入-购进成本)
如图,Rt△ABC中,∠C=90o,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
(1)求证:BE平分∠ABC;
(2)若CD︰BD=1︰2,AC=4,求CD的长.
如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,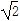 ≈1.41,
≈1.41,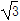 ≈1.73)
≈1.73)