若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知a,b是实数,1和-1是函数f(x)=x3+ax2+bx的两个极值点.
(1)求a和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
已知函数f(x)的图象与函数h(x)=x+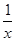 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若g(x)=f(x)·x+ax,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
设集合A={x|x2<4},B={x|1<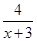 }.
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
已知数列{an}的前n项和Sn=-an- n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式.
(2)设数列 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn>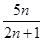 .
.
(3)设数列{cn}满足an(cn-3n)=(-1)n-1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有cn+1>cn.
已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),数列{bn}满足b1=1,且点P(bn,bn+1)(n∈N*)在直线y=x+2上.
(1)求数列{an},{bn}的通项公式.
(2)求数列{an·bn}的前n项和Dn.
(3)设cn=an·sin2 -bn·cos2
-bn·cos2 (n∈N*),求数列{cn}的前2n项和T2n.
(n∈N*),求数列{cn}的前2n项和T2n.